A Better SNT?

SNT is too conservative. Can and should we fix that?

Figure 1. Focus on D which shows the response in RIFs to a 15 minute pulse. The repair process is over in about 2 hours for 100 mGy, and 20 hours for 2000 mGy.\cite{bissell-2011}

Could SNT be improved? Made more realistic? Absolutely. Here are two obvious improvements.

1) Dose rate dependent repair period.

2) Stepped high end.

Dose Rate Dependent Repair Period

We know from the Berkeley work, Figure 1, that the DNA repair period depends on the number of Double Strand Breaks (DSB) which the cell has to deal with, which in turn depends on the dose rate. The effect was not subtle. A factor of 20 increase in the acute dose increased the repair period by a factor of 10.

We have good reason to believe that the primary problem is closely spaced Double Strand Breaks (DDSB's) which can be viably misrepaired be rejoining the wrong ends. If the probability of a DSB in a particular target area within a repair period is p, then the probability of two DSB's in that area is p^2. For a fixed repair period, this would point to a quadratic dose rate response. The effect of a dose rate dependent repair period will be an increase in the exponent, creating a sharper hook.

Figure 2. DDSB's generated by Monte Carloing a simple slot model. Two unrepaired hits in the same slot is called a DDSB, The right frame assumes a constant repair period. In the left frame, the repair period increases linearly with the number of DDSB's.

I confirmed this with a simple Monte Carlo model, Figure 2. On the left, I modeled the creation of Double DSBs (two unrepaired hits in the same slot) as a function of dose rate with a fixed repair period. As expected, the number of DDSB's increased quadraticly with dose rate, proxied by the hits per time tick. But when I assumed the repair time increased linearly with the number of DSB's on the right, then the response was a bit steeper than cubic.

This matches Rowland's observation that a cubic curve fits the radium dial painter data far better than a quadratic. Rowland dismissed his own finding:

Here the numerical value of the exponent has to be in the range 2.7 to 4.1, with the value 3.15 for the exponent appearing to be the best fit to the [dial painter] data. Needless to say, it is difficult to find any physical meaning for such a dose response function.\cite{rowland-1996}[page 3]

Hey, Bob, SNT with a repair period that increases with dose rate implies a better than cubic dose response function. Ignoring the data because you don't have an explanation for it has a long tradition in science.¹

A dose rate dependent repair period would allow up to do a much better job of fitting the radium dial painter data without worsening the fit to the atom bomb survivors.

Stepped High End

Cancer starts with a viable misrepair. It is reasonable to assume that, if a cell's DNA is too badly damaged, it becomes unrepairable, correctly or incorrectly. The cell dies or at least is unable to replicate, and no cancer results.

This picture is supported by the high end data in the atom bomb survivor cohort, the radium dial painters, and childhood thyroid cancer after Chernobyl. In every case, the top end cancer incidence flattens out far below 1.00, usually in the 0.3 to 0.5 range. This flattening occurs in the 50 to 100 mSv/day dose range.

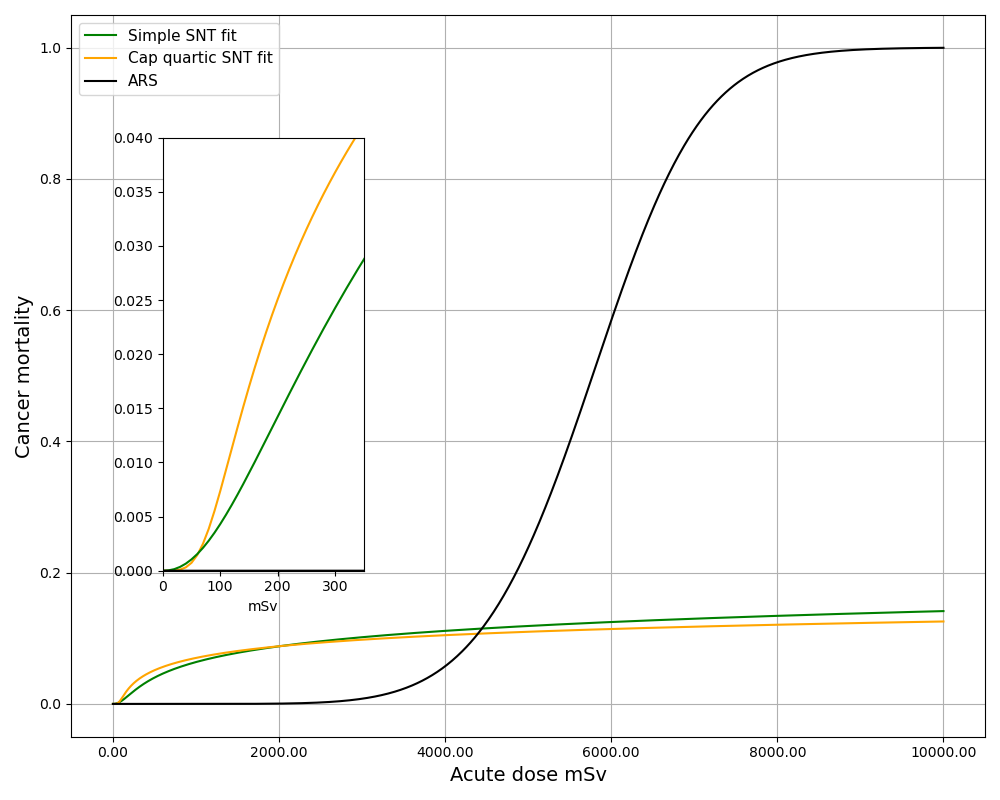
Our bodies can handle the loss of lots of cells. But if too many cells are killed too quickly, we see clinical harm: vomiting, tanning, sharply depressed immune system, etc. These symptoms are collectively known as Acute Radiation Syndrome. We start to see these problems around an acute dose of 1000 mSv. If the body is too damaged to adequately replace the lost cells, then death will result. At around 5000 mSv acute, we hit a mortality of 50%. At 10,000 mSv acute, the dose is almost always fatal. Figure 3 shows the ARS mortality among the Chernobyl first responders. It should come as no surprise that the response is S-shaped.

Figure 3. ARS Mortality Chernobyl First Responders

There is a sizable dose rate range between the flattening out of the cancer incidence (and mortality) and the onset of ARS. This leads to a stepped acute dose response curve, such as sketched in Figure 4. (We can't see the low end hooks in the SNT curves in the main figure, but they are there as the inset shows.) Implementing such a stepped response would not be difficult. It's just the sum of two S's, less their intersection, since cancer can't kill the people who have already been killed by ARS, Of course, the ARS curve would have a much longer repair period.

Figure 4. Stepped acute dose response curve. The total mortality curve is the max of the ARS curve and the chosen SNT curve.

Should we switch?

The flat region at the high end could be very important for plant workers and responders in a nuclear power power plant release. At Fukushima, around 10 workers suffered daily doses over 100 mSv. At Chernobyl, that number is in the thousands. But, with adequate buffer zones, the public will almost never experience daily doses in excess of 10 mSv. If and only if our simple SNT model is used only for the public, we can forego this complication with almost no practical implications.²

The dependence of the repair period on dose rate is not so easy to dismiss. We know its real. Over-estimating radiation harm will result in additional harm elsewhere. Nuclear power will be more expensive and that will result in a decrease in real wealth which has all sorts of negative implications, especially for the poor.

One counter argument is the dial painter dose was largely alpha particle. The public dose in a nuclear plant release will be almost all photon with some electron early on. Alpha particle damage is High LET (Linear Energy Transfer), far more localized, than Low LET photon and electron damage, and more likely to create Double DSB's and hence viable misrepairs. We would expect a higher exponent for high LET damage.

Unfortunately, I think we need more high dose rate, low LET data, before we can compellingly move to a more aggressive S. The obvious place to look for this data is the Chernobyl liquidators and the Fukushima workers. But in both cases the nuclear establishment won't tell us the all important dose rate profiles. Until they do, I'm afraid we will have to stick with the current overly conservative SNT model.

1. Recent examples are Wegener's crazy idea that America, Africa, and Europe were once a single continent. Or Bretz's nutty theory that a flood carved out the Columbia River Gorge in a matter of hours. Both were supported with oodles of evidence. Both were dismissed because the dismissers had no explanation for the data.

2. Look at Figure 4. It is intriguing that a 5 parameter logistic fit to the atom bomb survivor data results in a very large, shallow, upper hook. This means that the mortality from a single daily dose is effectively capped. But if those very large daily doses are repeated more than a couple of times, simple SNT fairly quickly approaches a mortality of 1.0.