The Probability of Exceeding the NRA Insurance Cap

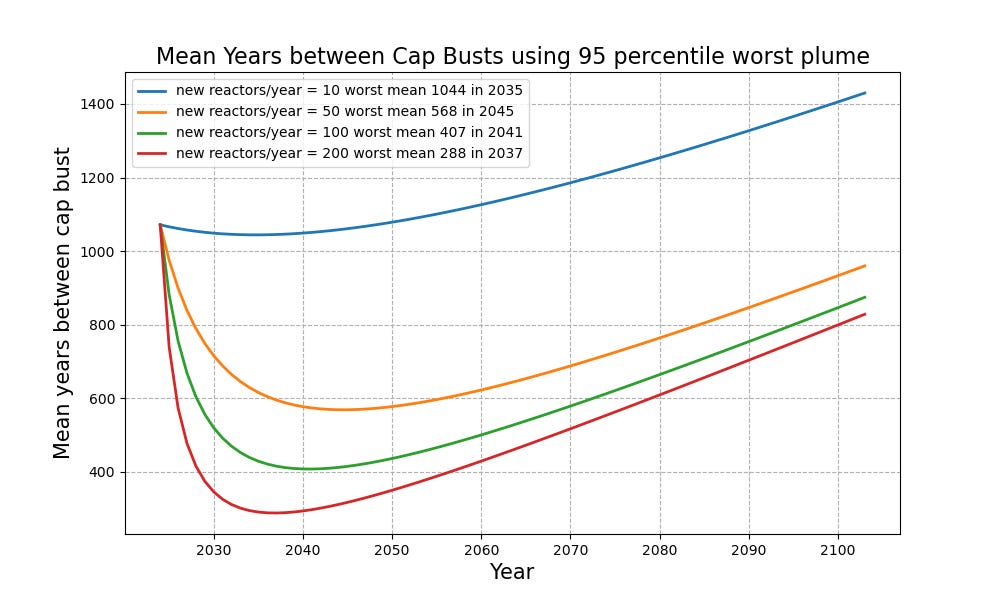
Figure 1. Mean Time Between Cap Exceedances assuming no more Chernobyls

Under the Nuclear Reorganization Act (NRA), the setting of the liability insurance required for a plant is a mechanical, technology agnostic process. To oversimplify slightly, the Nuclear Monitoring Agency(NMA) assumes a Chernobyl sized released in the 95% percentile worst case weather pattern seen at that site in the last ten years. 19 out of 20 times this release will produce a lower total compensation. For this plume and the population distribution around the plant, the NMA computes the amount of compensation that the NRA would require in this scenario. This calculation is updated every five years to account for changes in the population distribution.

If the NRA compensation in an actual release exceeds this cap, we taxpayers are on the hook. In thinking about the risk of this happening, it is important to emphasize that, under the NRA, radiation exposure compensation depends only on the maximal dose rate profile each individual would experience if he stood outside his home unmasked for 24/7 during the entire release. The compensation is automatic. There is no need to show any harm. Importantly, it is exclusive and unappealable. The NMA will measure the plume, compute your compensation using your SNT based Lost Life Expectancy, and cut you a check. That's it. No running to an ambulance chaser to get more. This means, for a given plume and population distribution, the total compensation is fixed and calculable. This not only makes nuclear commercially insurable; it allows us to estimate the probability that the cap is exceeded.

So far we have had about 22,500 reactor operating years. During that period, we have had one Chernobyl sized release. The second largest release, Fukushima, was at least ten times smaller, which for a better than quadratic harm model such as SNT results in a total compensation that is roughly 150 times smaller. The NRA cap combines a Chernobyl sized release with a weather pattern whose compensation will be exceeded 5% of the time. So, assuming no improvement in our ability to prevent releases, the probability of exceeding the cap is (1/22500) * 0.05 = 0.00000022 per reactor-year.¹ Right now, we have about 420 operating power reactors, so the probability of busting through the cap this year is 0.00093, or 1 capbust on average very 1071 years. I suggest that's clearly acceptable in return for the benefits of cheap nuclear.

The problem is, if we are to solve energy poverty and put a real dent in global warming, we are going to need a lot more nuclear plants, a whole lot more. If we come to our senses very quickly, the GKG suggests that an extremely aggressive but doable and non-destructive goal, if and only if we have should-cost nuclear, is Net 50 by 2100. This would require an essentially all nuke grid (along with current hydro and a bit of fossil for peaking and handling unplanned outages). This would decarbonize roughly 25% of primary energy. To get to 50%, we would need to electrify another 25%.

The GKG plan provides everyone with 800 watts of power (European average) by 2100. We can expect a 2100 population of about 10 billion humans. So to do that we need 8000 GW's of power or 8000 large reactors, or 7600 additional reactors over the next 75 years, or 100 new reactors per year. To electrify another 25% of primary energy, we would have to double that number. Now we are talking 200 reactors per year, 4 additional big reactors every week for 75 years. Sounds crazy; but nuclear plants do not consume a lot of resources. People like ThorCon have laid out a plan for doing just that. The obstacle is autocratic, monomanical regulation. To actually get this done, we must make a drastic change in how we regulate nuclear. We Can Make Nuclear Cheap Again outlines what we must do.

Assuming for the moment that we can pull that off, what does than mean for the probability of exceeding the NRA insurance cap? For the aggressive build ups, the number of nuclear plants will grow very quickly, and with it the probability of exceeding the cap. But something else is happening. We are gaining experience. Each year we do not have another Chernobyl decreases our probability of having a Chernobyl. Figure 1 shows how these two competing effects balance out as a function of the build rate. I've plotted the mean time between exceedances (the inverse of the annual probability) because for most people (including me who taught probability) it's more meaningful.

At very low build rates, the experience factor dominates. The time between capbusts dips very slightly before increasing. However, at the high build out rate required by Net 50 by 2100, the number of plants initially grows much faster than our experience. The probability of busting the cap increases and the average time between capbusts dips below 300 years. But if we continue to see no Chernobyl, eventually that experience overwhelms the plant growth; and the average time between capbusts start to go back up.

In the real world, we can't go to four additional big nukes a week right way. Even a dreamer like me will admit it will take us a decade or two to get there. In this case, the initial dip will be much smaller, and we will see an intermediary trajectory. I'm a fairly high bracket taxpayer; and overall I'm comfortable with the Figure 1 gamble. I think the cap is set about right. But that's not my call; it's Congress's. Do they have the guts to make it?

1. For the nerds, I'm assuming a Poisson process in which the explanatory variable is reactor-years, with a non-informative conjugate prior. In plain English, the simplest possible model.